10223. Поселенцы Катана

В игре года 1995 года в “Поселенцах Катана” игроки пытаются доминировать на острове строя дороги, поселения и города в неизведанной пустыне.

Вы работаете в компании – разработчике программного обеспечения, которая только что решила разработать компьютерную версию в этой игре, и Вы выбраны для реализации одного из особых правил игры:

По окончании игры игрок, построивший самую длинную дорогу, получает два дополнительных победных очка.

Проблема в том, что игроки обычно строят сложные дорожные сети, а не только один линейный путь. Следовательно, определение самой длинной дороги не является тривиальным делом (хотя игроки люди обычно видят это сразу).

По сравнению с оригинальной игрой, здесь мы рассмотрим упрощенную задачу: Вам предоставляется набор вершин (городов) и ребер (дорог) длины 1, соединяющих вершины. Самая длинная дорога определяется как самый длинный путь в сети, в котором не используется ребро дважды. Однако вершины можно посещать более одного раза.

Вход. Содержит один или несколько тестов. Первая строка каждого теста содержит два целых числа: количество вершин n (2 ≤ n ≤ 25) и количество ребер m (1 ≤ m ≤ 25). Следующие m строк описывают m рёбер. Каждое ребро задается номерами двух вершин, соединенных им. Вершины пронумерованы от 0 до n – 1. Ребра неориентированные. Вершины имеют степень три или меньше. Сеть не обязательно является связной. Ввод завершается двумя 0 для n и m.

Выход. Для каждого теста в отдельной строке выведите длину самой длинной дороги.

Пример входа	Пример выхода
3 2 0 1 1 2 15 16 0 2 1 2 2 3 3 4 3 5 4 6 5 7 6 8 7 8 7 9 8 10 9 11 10 12 11 12 10 13 12 14 0 0	2 12

РЕШЕНИЕ

графы – перебор

Анализ алгоритма

Запускаем поиск в глубину из каждой вершины. Генерируем все возможные пути, используя бектрекинг. Ограничение на количество вершин (n ≤ 25) позволяет уложиться в отведенное время. Находим длину наибольшего пути.

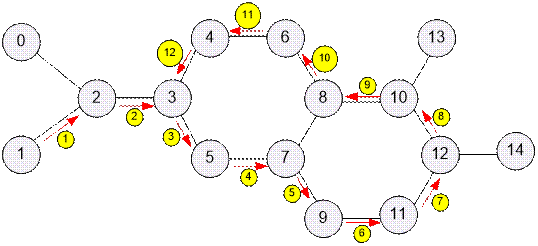
Пример

Во втором примере самый длинный путь имеет длину 12.

Реализация алгоритма

Объявим матрицу смежности графа mas.

#define MAX 26

int mas[MAX][MAX];

Заходим в вершину i. Текущее расстояние от начальной вершины до i равно depth.

void run(int i, int depth)

{

В переменной best поддерживаем значение самого длинного пути.

if (depth > best) best = depth;

Ищем, в какую вершину j можно попасть из i.

for (int j = 0; j < n; j++)

if (mas[i][j])

{

Удаляем ребро (i, j) и продолжаем поиск из вершины j.

mas[i][j] = mas[j][i] = 0;

run(j, depth + 1);

По возвращению из функции run восстанавливаем ребро (i, j).

mas[i][j] = mas[j][i] = 1;

}

}

Основная часть программы. Обрабатываем несколько тестов.

while (scanf("%d %d", &n, &m), n + m)

{

memset(mas, 0, sizeof(mas));

Читаем входные данные. Строим граф.

for (i = 0; i < m; i++)

{

scanf("%d %d", &a, &b);

mas[a][b] = mas[b][a] = 1;

}

Запускаем поиск в глубину из каждой вершины. Вершины пронумерованы от 0 до n – 1. В переменной best вычисляем максимальную длину пути.

best = 0;

for (i = 0; i < n; i++)

run(i, 0);

Выводим ответ.

printf("%d\n", best);

}

Java реализация

import java.util.*;

public class Main

{

static int g[][] = new int[26][26];

static int n, m, best;

static void run(int i, int depth)

{

if (depth > best) best = depth;

for (int j = 0; j < n; j++)

if (g[i][j] == 1)

{

g[i][j] = g[j][i] = 0;

run(j, depth + 1);

g[i][j] = g[j][i] = 1;

}

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

while(true)

{

n = con.nextInt();

m = con.nextInt();

if (n == 0 && m == 0) break;

for (int i = 0; i < 26; i++)

Arrays.fill(g[i], 0);

for (int i = 0; i < m; i++)

{

int a = con.nextInt();

int b = con.nextInt();

g[a][b] = g[b][a] = 1;

}

best = 0;

for (int i = 0; i < n; i++)

run(i, 0);

System.out.println(best);

}

con.close();

}

}